埃舍尔的艺术及其与科学的关联：绘画就是“欺骗”

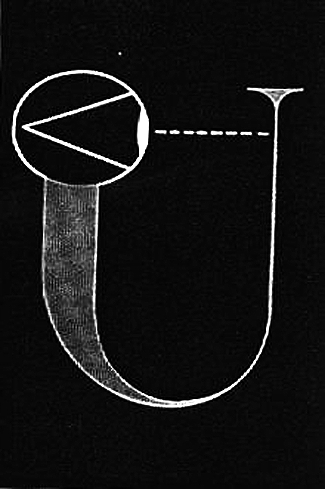
图7:惠勒:参与者的宇宙图示

摩里茨·科奈里斯·埃舍尔

埃舍尔是一位个性鲜明、画风独特的艺术家。直到今天,他在数学、物理学等领域的影响要比在艺术界大得多。他以其他艺术家表达情感的方式表达理性,他的每一幅画都隐藏着他对画面本身的思考,而他所思考的问题以及思考、解决问题的方式与科学家更为相似。在某种意义上甚至可以说,埃舍尔是以科学家的方式进行艺术创作的。

1、无穷,数学曲线与平面上的探索

埃舍尔说,绘画就是“欺骗”!

他注意到,我们的现实空间是三维的,而所有的平面艺术都是二维的。他认为:现实的三维世界和它的二维平面表达之间,不可能存在一一对应的关系,画家在二维空间所画的,只能是三维现实空间中实际物体的一部分,而大脑则通过这个部分想象其完整情形。既然视知觉能把画布上的线条和形体想象为三维空间中存在的物体,那么,是否有可能在画布上制造一个看似三维但在现实三维空间中又不可能存在的物体呢?

终其一生,埃舍尔都在挖掘、探索、扩展平面表达的可能性。

1959年,埃舍尔开始思考这样一个问题:世界和宇宙是无穷的,为什么没有画家表现无穷呢?假如有,会是什么方式呢?埃舍尔不满于用抽象的、混沌的色彩来表现无穷。他说:“如果我们想建构一个宇宙,不能让它是模糊不清的抽象物,而必须是可以识别的具体形象。让我们用无数形状相似,同时又明晰可辨的建筑模块来构造一个二维的宇宙吧!”

埃舍尔发现了法国数学家彭加勒为了表现双曲几何而发明的图形,他马上意识到这个结构可以用来表现无穷。他摸索了很久,制作了被称为“考克斯特类”的作品。他最得意的是《圆极限III》(图⑥),他写道:“一串串鱼像火箭一样,从无穷远的边缘以直角发射出来,又跌落到所来的地方,没有一条鱼能最终到达边缘。因为在那之外是‘绝对的无’。然而,这个圆的世界如果没有周围的虚空也不可能存在,不仅仅因为‘内’的前提是‘外’,而且因为,由这种几何精确地指定的、建构起整个框架的圆弧的圆心,就在‘无’的领地之中。”

埃舍尔最后一幅重要的作品《蛇》中也包含有考克斯特结构。在《蛇》的画面中,三条蛇穿行于圆环中。圆环的分布和变化有考克斯特的形状,但又有所变化。这个结构最特殊的地方在于,这些圆环可以不断地向内延伸,达到无穷小,也可以不断地向外延伸,达到无穷小。

埃舍尔还制作了很多纯粹以数学图形为对象的作品。比如《默比乌斯带》、《群星》、《旋》等。《旋》是一个特殊的数学结构,一个自身缠绕的不断向内的旋转螺线。这种数学韵味十足的结构是埃舍尔所痴迷的既抽象又具体的对象。埃舍尔创造的这种新的结构,也激起了数学家的强烈兴趣,给埃舍尔的结构一个数学表达,成为数学家的一个智力活动。

埃舍尔甚至还有超出数学家的发现。在《天使与魔鬼》中,埃舍尔表现了三种对称性:旋转对称,镜射对称,还有一种连数学家也不常遇到的对称性——滑移反射对称。这种对称在晶体结构中有具体的表现,有晶体学家还专门写了一本《论埃舍尔周期性绘画中的对称》,供晶体学专业的学生使用。

转载旨在分享，文章、图片版权归原作者所有，如有侵权，请联系我们进行删除。